Non-Numbers and the Birth of Calculus

The story of another candidate for numberhood, the infinitesimal, is even stranger than the story of the irrationals or the imaginaries. The infinitesimal is the limit of a process, where the method stipulates that the end of that process can never be reached. Consider: can a single mathematical point have a slope? Our intuitive answer, trained by Euclid, is: no. A point is pure position. It isn’t a line, it isn’t even a tiny part of a line, so it can’t have a slope!

Can there be a smallest possible line?  How short can a line get and still have a slope!

That’s a question that Euclid taught us not to ask. It is akin to suggesting that we can have two adjacent points. If we could have two adjacent points, then they would presumably constitute the smallest possible line and they would have a slope. But we can’t. Between any two points, properly speaking, infinity of other points can fit.

In the seventeenth century it was common for the mathematicians at its cutting edge to speak as if they were postulating lines of “infinitesimal” length. Real length, greater than a point, but ever so small, the end of a process of shortening lines, while they remain in a genuine sense lines. The limit of a process that cannot end … that is an infinitesimal.

John Wallis invented the term, in 1655, and used this quasi-numerical symbol for it:   .

Wallis’s writing wasn’t quite “calculus” as that term is now understood, but he was knocking on the door. Newton and Leibniz both walked through that door in the 1680s, and although they were working independently of one another, each was indebted to Wallis. Newton described his own methods as using “one or more measures of the infinitesimally small” in a 1684 work, De motu corporum in gyrum (“On the motion of bodies in an orbit.”) Newton also created the word “fluxion” as part of his effort to describe motion within the strange new language developing for calculus.

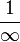Whenever there is a new sort of number, as we’ve learned, there are skeptics. There are those who want nothing to do with the new numbers, and others who might want to deal with it secretly, shamefacedly, simply when necessary to avoid mental torture.

The great skeptical attack on infinitesimals was that launched in the following century, in the year 1734, by philosopher George Berkeley, in a pamphlet called The Analyst: A Discourse Addressed to an Infidel Mathematician.  And as it happens, given the rather imprecise ways in which the premises of calculus were espoused in those days, Berkeley had a point. No pun intended. He wrote:

 “And what are these Fluxions? The Velocities of evanescent Increments? And what are these same evanescent Increments? They are neither finite Quantities nor Quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities?”

 Yes, under the rules of geometry this tiny line that was just a point, yet somehow more than a point, was impossible. A number or notation that denoted such a thing was itself also an absurdity, just like … well … just like a decimal number that never ends or finds a repeating pattern … just like a square root of a negative number.

Yet by pretending that something that couldn’t exist under the previous rules nonetheless can exist, we establish new rules and a new game, and perhaps in the process we figure out how planetary orbits work. Pragmatism triumphs over conceptual quibbles.

There are a couple of more twists and turns here, though.

In the 19^th century, Karl Weierstrass banished the weird infinitesimals, and in the middle of the 20^th century, Abraham Robinson would try to bring them back.

Weierstrass gave a series of lectures in 1859-60 in which he reinterpreted the notion of limits and tangents so they no longer required infinitesimals. You could acknowledge Berkeleyan objections without abandoning Newton’s accomplishments. Since then, historians of the field have said that Weierstrass laid the correct “foundations” for the field. But is this really so or was his achievement a matter of cosmetics?

That’s the question Robinson raised, beginning with a seminar he ran at Princeton in 1960, and culminating in his book, Non-standard analysis. Robinson contended that the form of calculus, a/k/a analysis, that had become standard since Weierstrass’ day was unnecessarily cumbersome and thus unnecessarily difficult to teach. He proposed a return to the ideas of the founders (he was thinking more of Leibniz than of Newton). Those ideas, he said, imply “the introduction of ideal numbers which might be infinitely small or infinitely large compared with the real numbers,” and these ideas can be “fully vindicated.” 

 Robinson’s ideas continue to excite discussion in the early 21^st century, so it is possible “ideal numbers” shall see full citizenship someday, though in the meantime calculus progresses in Weierstrassian fashion without them.